Machine Learning Basics
Machine Learning is the field of study that gives computer the ability to learn without being explicitly programmed. A computer program is said to learn from experience E with respect ot some task T and some performance measure P, if its performance on T , as measured by P, improves with experience E.
Machine Learning Algorithms:
- Supervised Learning
- Regression (continuous output)
- Classification (discrete valued output)
- Unsupervised Learning
Linear Regression
Linear Regression with one variable
\( Hypothesis : h_{\theta}(x) = \theta_{0} + \theta_{1}x \)
\( Parameters : \theta_{0}, \theta_{1} \)
\( Cost function : J(\theta_{0}, \theta_{1}) = \frac{1}{2m}\sum\limits_{i=1}^{m}(h_{\theta}(x^{i}) - y^{i})^2 \)
\( Goal : Minimize : J(\theta_{0},\theta_{1}) \)
Gradient descent
Repeat until covergence
{ \( \theta_{j} := \theta_{j} - \alpha\frac{\partial}{\partial\theta_{j}}J(\theta_{0}, \theta_{1}) \)} (for j=0 and 1)
\( \theta_{0} := \theta_{0} - \alpha\frac{1}{m}\sum\limits_{i=1}^{m}(h_{\theta}(x^{i}) - y^{i}) \)
\( \theta_{1} := \theta_{1} - \alpha\frac{1}{m}\sum\limits_{i=1}^{m}(h_{\theta}(x^{i}) - y^{i})x^{i} \)
Linear Regression with multiple variable
\( Hypothesis : h_{\theta} = \theta^{T}x = \theta_{0}x_{0} + \theta_{1}x_{1} + . . . \theta_{n}x_{n} \)
\( Parameters : \theta = [ \theta_{0}, \theta_{1}, \theta_{2}, . . \theta_{n} ]^T \)
\( Cost function : J(\theta) = \frac{1}{2m}\sum\limits_{i=1}^{m}(h_{\theta}(x^{i}) - y^{i})^2 \)
Gradient descent
Repeat until convergence
{\( \theta_{j} := \theta_{j} - \alpha\frac{\partial}{\partial\theta_{j}}J(\theta) \)} (simultaneously update for every j=0,1,2…n)
\( \theta_{j} := \theta_{j} - \alpha\frac{1}{m}\sum\limits_{i=1}^{m}(h_{\theta}(x^{i}) - y^{i})x^{j} \)
Method to solve of \( \theta \) analytically : Normal Equation
Let \( h_{\theta} = \theta^{T}x = \theta_{0}x_{0} + \theta_{1}x_{1} + . . . \theta_{n}x_{n} \)
\( \implies (\theta^Tx)^T = Y \)
\( \implies x\theta^T = Y \)
\( \implies x^Tx\theta^T = x^TY \)
\( \implies \theta^T = (x^Tx)^{-1}x^TY \)
Logistic Regression
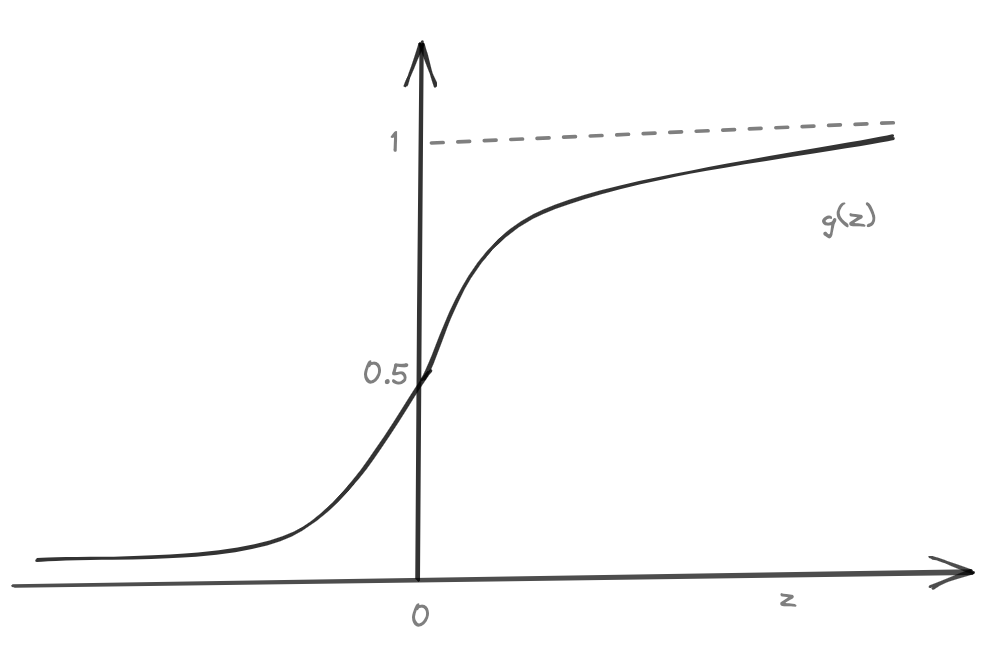
In Logistic regression, \( 0 \le h(\theta) \le 1 \)
In Linear regression, \( h(\theta) = \theta^Tx \in (R) \)
In Logistic regression, \( h(\theta) = g(\theta^Tx) \)
where,
\( \ \ \ \ \ \ \ g(z) = \frac{1}{1 + e^{-z}} = sigmoid/logistic function \)
\( \implies h_{\theta}(x) = \frac{1}{1 + e^{-\theta^Tx}} \).
\(h_{\theta}(x) \) = estimated probability that y=1 on input x.
i.e., \(h_{\theta}(x) = P(y=1|x;\theta) \) = prob. that y=1, given x, parameterzed by \(\theta \).
Now; \( h_{\theta}(x) = 0.5 \)
\(\implies \frac{1}{1 + e^{-\theta^Tx}} = 0.5 \)
\( \implies \theta^Tx = 0\)
so, \(h_{\theta}(x) \ge 0.5 \implies \theta^Tx \ge 0 \)
and, \(h_{\theta}(x) \le 0.5 \implies \theta^Tx \le 0 \)
Ex. Let \(h_{\theta}(x) = g(\theta_{0} + \theta_{1}x_{1} + \theta_{2}x_{2}) = g(\theta^Tx) \) (at \( \theta=[-3,1,1] \))
\( \implies Predict \ y if \ -3 + x_1 + x_2 \ge 0 \)
\( \implies x_1 + x_2 \ge 3 \) (Linear decision boundary)
Cost function for logistic regression
\( J(\theta) = -\frac{1}{m}\sum\limits_{i=1}^{m}[y^{i}log(h(x^{i},\theta)) + (1-y^{i})log(1-h(x^{i},\theta))] \)
Following to to be completed . . .